Nous souhaitons accompagner tous les enseignants qui, comme nous, croient en l'efficacité de la méthode de Singapour pour enseigner les mathématiques au primaire.
Vous trouverez sur cette page tous les outils et toutes les ressources que nous mettons à votre disposition afin de vous aider à mettre en œuvre la méthode auprès de vos élèves.
Les mathématiques s'adressent à tout le monde. La méthode de Singapour permet à chacun d'atteindre un profond niveau de compréhension.
L'accent est mis sur le sens : la priorité est donnée à la réflexion et au raisonnement, et non à la mémorisation par cœur de procédures de calcul. La résolution de problèmes est au cœur de l'enseignement.
Les élèves apprennent à penser mathématiquement et à s'appuyer sur la profondeur des connaissances acquises dans les leçons précédentes.
Cette stratégie repose sur 3 représentations : Concrète, Picturale (ou Imagée) et Abstraite. Elle est la colonne vertébrale de la méthode de Singapour.
Avec X’bouc, l'outil numérique permet à l'enfant de manipuler n'importe quel objet, y compris des pommes et des bananes !
La représentation picturale établit un pont entre les représentations « concrètes » et « abstraites » du problème, afin d'aider les enfants à relier les objets physiques à l’algorithme.
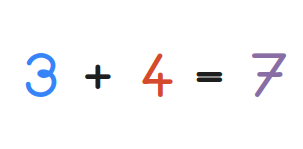
Utilisation des symboles mathématiques pour représenter le problème par une équation.
L'enfant progresse d'une représentation à une autre, et revisite les étapes chaque fois que nécessaire pour renforcer son apprentissage.
Cette approche est critique pour aider les enfants à comprendre le sens des nombres et construire des fondations solides.
Un mariage de nombres est un outil pictural qui montre les relations parties-tout entre les nombres.
En tant que représentation picturale, il fait le pont entre la manipulation physique des nombres et la compréhension conceptuelle des opérations arithmétiques de l'addition et de la soustraction.
Grâce à l'utilisation répétée des mariages de nombres, l'élève acquiert un sens solide des nombres qui lui servira tout au long de son éducation mathématique.
Dans X’bouc, vous pouvez créer en quelques clics un exercice avec des mariages de nombres à compléter.
Les mariages de nombres aident les enfants à passer de la compréhension concrète à la compréhension abstraite. Ils sont l’étape entre la manipulation physique des nombres et la compréhension conceptuelle des opérations arithmétiques d’addition et de soustraction.
Le modèle en barres est une stratégie efficace de résolution de problèmes.
Il permet aux enfants de créer une représentation visuelle des problèmes.
Peux-tu trouver les parties et le tout ? Construis un modèle pour t'aider à résoudre ce problème.
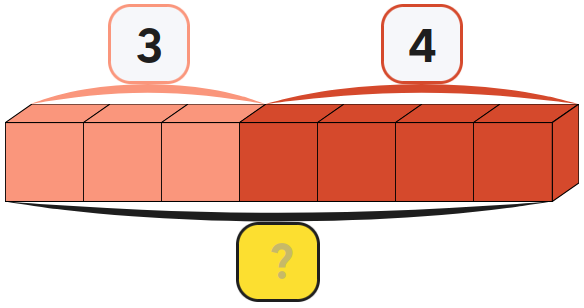
L'enfant crée un modèle qui correspond aux données du problème. Le modèle permet de visualiser les quantités.
L'enfant écrit et résout une équation associée au modèle.
Retrouvez dans X’bouc des séquences de résolution de problèmes prêtes à l'emploi basées sur le modèle en barres. Du CE1 à la 6ème, les exercices s'adaptent automatiquement au niveau de vos élèves et permet à chacun d'avancer à son rythme.
Les séquences s'appuient également sur la typologie des problèmes de Vergnaud pour assurer une homogénéité des problèmes proposés.
Ce sont les grandes idées dans chaque domaine des mathématiques, telles que l'algèbre, la géométrie et les statistiques.
Ce sont les outils mathématiques de base. Certaines compétences requièrent de la manipulation, comme utiliser un rapporteur ou une règle pour mesurer. D'autres compétences sont plus abstraites, comme la visualisation spatiale ou l'analyse de données. Et les compétences qui nous sont probablement plus familières sont procédurales, comme des calculs simples impliquant l’addition, la soustraction, la multiplication et la division.
C'est faire des maths. Quand on fait des maths, nous raisonnons, faisons des connexions, et nous communiquons. Faire des maths est une activité très engageante et très active, impliquant les élèves dans l’échange d’idées.
Elle consiste à réfléchir sur sa propre pensée. Cela exige que les élèves réfléchissent constamment aux concepts, aux compétences et aux processus mathématiques, en se demandant continuellement ce qui a du sens, quelles procédures fonctionneront et ce qui pourrait prouver que notre réflexion est fausse.
C'est l'état d'esprit nécessaire pour être un penseur critique et un résolveur de problèmes. Une bonne éducation mathématique crée un appétit pour la résolution de problèmes et un amour de l'apprentissage des mathématiques.
